Instantaneous Spectral Analysis

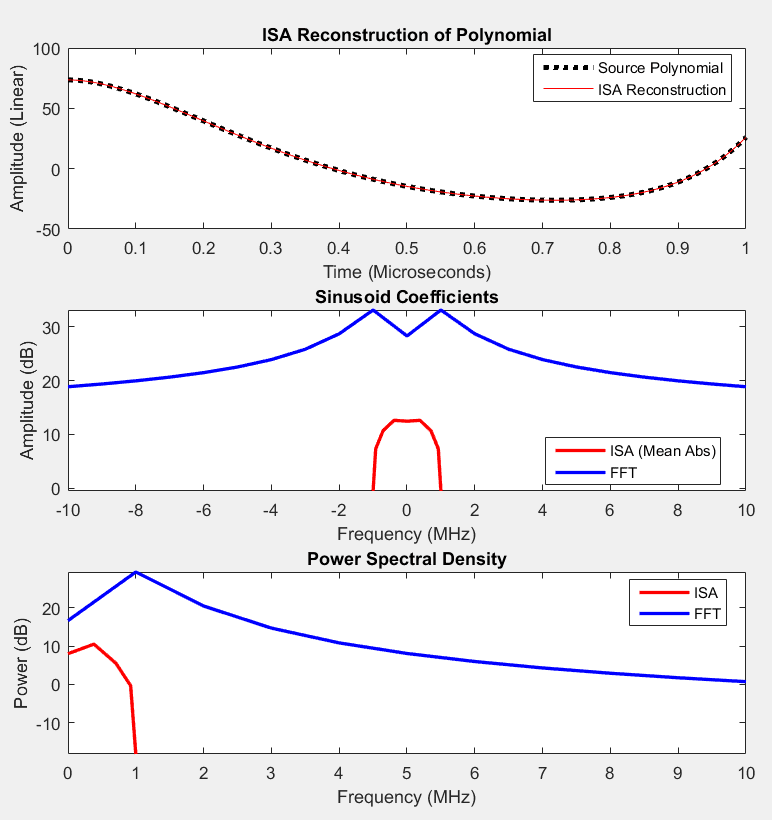
Arising from the underlying mathematics for Spiral Modulation is a technique called “Instantaneous Spectral Analysis” (ISA). ISA shows that any waveform can be represented in terms of sinusoids with continuously-varying amplitude, in such a way that power is put into a much smaller range of frequencies than has traditionally been believed to be possible.

A peer-reviewed published paper on ISA is available here.

The classical Fourier transform, which is based on Euler’s formula, converts a waveform into a sum of sinusoids each of which has constant amplitude. ISA, which is based on a generalization of Euler’s formula, removes the constraint that the sinusoidal amplitude must be constant. Since removing a constraint always removes a cost, ISA allows for a much more spectrally-efficient representation of a waveform than can be produced by a Fourier transform.

Intuitively, the Fourier transform responds to more detail in the time domain by using higher frequencies. ISA instead responds by using more frequencies packed into the same range.

As the below chart shows for an arbitrary (random) waveform, ISA can cut the range of frequencies into which it puts power by 10X or more, as compared to the Fourier transform representation.