Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
This document provides brief answers to common questions about Astrapi technology for the benefit of communications engineers. More detailed information is available on our website at www.astrapi-corp.com/technolog, including performance data, white papers, and an overview of applicable intellectual property. No registration is required.
If you want to engage further with Astrapi, please reach out to us at [email protected]
Contents
Fundamentals
F1: How is Astrapi’s spiral-based signal modulation different?
F2: What are the benefits of Astrapi’s spiral-based signal modulation technology?
F3: Are Astrapi’s claims for dramatically higher spectral efficiency consistent with Shannon’s law?
F4: What form does Shannon’s law take for non-periodic signals?
F5: Can bandlimited spiral-based signals be fully reconstructed by sampling at the Nyquist rate?
F6: Intuitively, why are sampling rate and slew rate important for spiral-based non-periodic signal modulation?
F7: Doesn’t a high slew rate inherently mean high bandwidth usage?
F8: What is the engineering cost to implement spiral-based signal modulation?
F9: Are we backward compatible with QAM, PSK, GSM, etc.?
F10: How do I evaluate slew rate requirements for spiral-based signal modulation?
Design
D1: Can we bandlimit a non-periodic spiral-based signal?
D2: Do we require different/more expensive pulse-shaping filters?
D3: How do we know how much bandwidth we are using?
D4: How can we visualize spiral-based waveforms?
D5: What are our Forward Error Correction (FEC) requirements?
D6: How does spiral-based signal modulation perform with rain fade?
D7: How does it perform with coherent noise?
D8: Can we handle multipath interference?
D9: Can we handle clock recovery?
Systems Integration
S1: What are the power amplification linearity requirements for Astrapi spiral-based signal modulation?
S2: What product development support do we have available?
S3: Are the hardware components necessary to achieve a significant win with Astrapi technology available at a reasonable price?
__________________________________________________________

Fundamentals
F1: How is Astrapi’s spiral-based signal modulation different?
Astrapi has pioneered a new type of signal modulation based on complex spirals, rather than the traditional complex circles used by standard signal modulation techniques such as Quadrature Amplitude Modulation (QAM) and Phase Shift Keying (PSK). The approach arises from a new generalization of Euler’s formula, the underlying mathematics for the telecommunications industry.
F2: What are the benefits of Astrapi’s spiral-based signal modulation technology?
Spirals are the natural generalization of circles. Spirals can do everything that circles can do, but they can do new things as well. By moving from traditional circle-based signal modulation to Astrapi’s spiral-based signal modulation, there are more ways to distinguish between symbol waveforms, and as a consequence noise resistance can be greatly improved, for the same available bandwidth and signal-to-noise power ratio (SNR).
Traditional signal modulation techniques based on complex circles distinguish between symbol waveforms in some combination of three ways: amplitude modulation, frequency modulation, and phase modulation.
Spiral-based signal modulation can make use of the usual amplitude, frequency, and phase modulation, but adds three new possibilities: intra-symbol complex amplitude variation, rotational reversal, and time reversal.
The effect of improving noise resistance by transitioning to spiral-based signal modulation is that spectral efficiency can be driven dramatically higher: in principle, by a factor of ten or more for pure Additive White Gaussian Noise (AWGN) channels.
Dramatically higher spectral efficiency can be used to improve any combination of data throughput, bandwidth usage, signal power requirements, and error rate. There are potentially secondary benefits as well, such as lower Forward Error Correction (FEC) requirements, lower latency, better rain fade performance, improved performance against coherent and multipath interference, and reduced need for linear power amplification.
F3: Are Astrapi’s claims for dramatically higher spectral efficiency consistent with Shannon’s law?
Shannon’s law proves that for a specified amount of bandwidth and a specified SNR, there is a sharp limit on the maximum rate of error-free information transmission (the “channel capacity”). Existing signal modulation technology is already close to this limit.
However, Shannon’s proof used a mathematical technique that implicitly assumed that the signals were based on periodic functions, as has been standard industry practice. Since spirals are not periodic functions, a generalization of Shannon’s law is necessary to cover Astrapi’s spiral-based signal modulation.
While Astrapi’s spectral efficiency gains would be impossible if we were using symbol
waveforms based on periodic functions, they are predicted by the generalized non-periodic version of Shannon’s law and confirmed by simulation results.
F4: What form does Shannon’s law take for non-periodic signals?
In its familiar periodic form, Shannon’s law is
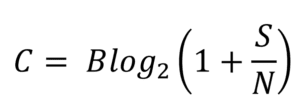
Where B is the available bandwidth, S/N is the SNR, and C is the channel capacity.
When generalized to non-periodic signals, Shannon’s law acquires a third parameter, which is related to slew rate (the maximum rate of amplitude change)
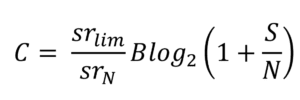
Here, ![]() is the ratio of the maximum slew rate the communication system can support
is the ratio of the maximum slew rate the communication system can support ![]() to the slew rate observed when the communication system operates at the Nyquist rate
to the slew rate observed when the communication system operates at the Nyquist rate ![]()
This tells us that spiral-based non-periodic signal modulation can out-perform traditional periodic signal modulation by a factor limited by the maximum slew rate that the communication system can support.
A full derivation is available from the Astrapi website.¹
F5: Can bandlimited spiral-based signals be fully reconstructed by sampling at the Nyquist rate?
In general, no.
The sampling theorem, proved by Shannon and others, shows that bandlimited periodic signals can be fully reconstructed by sampling at the Nyquist rate of twice the baseband frequency. However, Astrapi mathematics demonstrates that the same is not true for bandlimited non-periodic signals. In principle, it is possible to construct a bandlimited non-periodic signal that requires an arbitrarily high number of samples to fully reconstruct it.
The implication is that it is possible to transmit independent data points at a much higher rate using bandlimited non-periodic signals than using bandlimited periodic signals. This leads directly to the much higher channel capacity, and hence spectral efficiency, of non-periodic spiral-based signal modulation.
For further details, see Section 2 on the frequency of definition available in The Shannon Law for Non-Periodic Channels.¹
F8: What is the engineering cost to implement spiral-based signal modulation?
Fundamentally, Astrapi makes it possible to trade silicon (hardware performance) for spectral efficiency. This is only a win if silicon is relatively cheap, compared to spectrum. In particular, if it is a problem to drive the sampling rate and the slew rate higher than the minimum specifications for a tradition periodic signal modulation implementation, then Astrapi technology does not provide a benefit. In addition to the direct hardware costs of increasing the sampling rate and slew rate, pulse-shaping filter lengths become longer as spectral efficiency increases, and the demodulation analysis becomes more involved.
However, since silicon is becoming ever cheaper, and spectrum ever more expensive, Astrapi technology is relevant for an increasing number of applications. And the spectral efficiency win we provide for pure AWGN channels is linear with increasing sampling rate and slew rate.
F9: Are we backward compatible with QAM, PSK, GSM, etc.?
No. Spiral-based signal modulation is a sharp break from the past. Not only are we incompatible with existing signal modulation techniques, we are also incompatible with essentially all standards that cover signal modulation.
Astrapi believes that the first markets to adopt spiral-based modulation will be in applications for which spectral efficiency is very important (high data throughput requirements, limited signal power and limited bandwidth) and for which standards are not an issue, generally implying closed communication systems.
F10: How do I evaluate slew rate requirements for spiral-based signal modulation?
Non-periodic spiral-based signal modulation systems require slew rates exceeding the Nyquist slew rate in order to provide a spectral efficiency advantage over traditional periodic systems. It can be shown, for instance, that for a spiral-based signal modulation system to support a channel capacity of 100 Mbps through a 20 MHz channel with an 8 dB SNR requires a slew rate of 1.74 times the Nyquist slew rate.²
The slew rate of system components required to support a sinusoid of frequency ![]() with amplitude
with amplitude ![]() is the maximum rate of change of the signal, which is the maximum of the first derivative with respect to time.
is the maximum rate of change of the signal, which is the maximum of the first derivative with respect to time.
Slew rate (Nyquist) = ![]() = max
= max ![]() = max
= max ![]() Volts/second
Volts/second
The maximum rate of change for a sinusoid occurs at t = 0 . Evaluating the derivative of a sinusoid at t = 0 results in:
![]()
This is the minimum slew rate required for components to support a sine wave of frequency ![]() . Traditionally, this is the slew rate required to support Nyquist frequency based systems.
. Traditionally, this is the slew rate required to support Nyquist frequency based systems.
An RF transmitter delivering 1 watt into a 50 ohm matched load at 2.4 GHz would require a slew rate of ![]()
![]()
to support Nyquist systems.
Using spiral-based signal modulation to deliver a 100 Mbps information rate through a 20MHz
channel at 2.4 GHz with an 8 dB SNR would require a slew rate of 1.74 times the Nyquist rate or
5200 V/µsec.
Design
D1: Can we bandlimit a non-periodic spiral-based signal?
Yes. Spirals have the same frequency properties as circles, with the addition of complex amplitude variation. Traditional pulse-shaping filter technology can be applied to limit bandwidth usage.
In our primary design, we use the Gaussian pulse-shaping filter (like GSM) rather than the square-root raised cosine (SRRC) filter (like QAM and PSK). This is because of the performance benefits arising for spiral-based modulation from gathering as many data points as possible per symbol waveform, rather than the single point without inter-symbol interference that the SRRC filter provides. The Gaussian pulse-shaping filter is more efficient than the SRRC both in terms of performance and hardware costs.
D3: How do we know how much bandwidth we are using?
Bandwidth usage is bounded by running our signals through a Gaussian pulse-shaping filter. In our simulations, we check bandwidth usage with a standard Fast Fourier Transform (FFT), comparing ourselves to QAM or PSK for matched conditions.
The use of an FFT for non-periodic signals is somewhat suspect since the FFT is based on periodic sine and cosine waves. However, any mistakes made by the FFT will be in the direction of implying that we are using more bandwidth than we really are, rather than less. This is because the amplitude variation of a low-frequency spiral can be described with periodic sine and cosine functions only by using higher frequencies. So it is conservative to compare ourselves to QAM or PSK for the same measured bandwidth as determined by an FFT.
We have also confirmed our bandwidth usage with physical measurements using a sweep-and-hold technique that does not rely on a Fourier transform.
D4: How can we visualize spiral-based waveforms?
For periodic techniques such as QAM, each symbol is equivalent to a point in the complex plane (the “constellation diagram”). For spiral-based signal modulation, in general each symbol is equivalent to a sequence of points (a “trajectory”) that can be plotted in the complex plane.
D5: What are our Forward Error Correction (FEC) requirements?
For pure AWGN channels, it is preferable to implement spiral-based signal modulation with little or no FEC. The reason is that we can better use the bandwidth that FEC consumes to instead loosen our pulse-shaping filter, allowing us to get more clean, independent samples per symbol waveform. Our lower dependence on FEC implies lower latency than traditional signal modulation techniques, and that our performance decays gracefully with increasing noise, rather than exhibiting a catastrophic “FEC cliff” performance collapse.
Of course, there are conditions under which FEC is required, notably if there is burst noise with length approaching the symbol time.
D6: How does spiral-based signal modulation perform with rain fade?
Since spiral-based signal modulation has higher spectral efficiency than traditional signal modulation, it is less affected by the sudden decrease in the SNR caused by rain.
Additionally, to the extent that we are less dependent on FEC (see above) we do not have an “FEC cliff”: i.e., a sudden and catastrophically large increase in the error rate when the SNR drops below a certain level. Our performance decays gradually as noise builds. The signal power does not need to be kept unnecessarily high (or the data rate unnecessarily low) to provide a safety margin against the FEC cliff.
D7: How does it perform with coherent noise?
Spiral-based signals do not look like traditional periodic signals, which simplifies the problem of separating our signals out from competing channels. This provides us with an advantage against coherent noise. However, unlike for AWGN, a high sampling rate does not assist spiral-based signal modulation against coherent noise because more copies of the same noise do not help us to remove it.
D8: Can we handle multipath interference?
Spiral-based signal modulation has the same issues with multipath that other signal modulation techniques have. However, we have an advantage in that for a given data rate, we are less dependent on phase information, because we have additional ways of storing information. This means we are less affected by timing uncertainty.
D9: Can we handle clock recovery?
Spiral-based signal modulation has the same problems with clock recovery as do other signal modulation techniques, and the same solutions generally apply.
As with multipath interference, a relative advantage of spiral-based signal modulation is that it is less dependent on phase information, and therefore more tolerant of timing uncertainty. Additionally, spiral-based modulation (unlike QAM) is not dependent on a high degree of timing alignment in order to read a single point per symbol without inter-symbol interference.
Systems Integration
S1: What are the power amplification linearity requirements for Astrapi spiral-based signal modulation?
Spiral-based signal modulation supports new techniques for improving resistance to non-linear distortion. A spiral is a (real-valued) exponential multiplied by a complex circle. Since the growth characteristics of an exponential are well-understood, deviation from the exponential caused by non-linear distortion can be characterized on a per-symbol basis and corrected.
A disadvantage of spiral-based signals is that in general, they have higher peak-to-average power ratios (PAPR) than do traditional periodic signals. This means that for the same average power, spiral-based signal modulation will hit the non-linear region more often. However, PAPR is an adjustable parameter for spiral-based signals, and there are techniques for mitigating this issue.
S2: What product development support do we have available?
Astrapi provides foundational IP, world-leading expertise in the area of non-periodic signal modulation, and MATLAB® and Simulink® software models.
S3: Are the hardware components necessary to achieve a significant win with Astrapi technology available at a reasonable price?
Astrapi technology requires high sampling rates, high slew rates, and long filters in order to produce dramatic spectral efficiency gains. Fortunately, all of these components are increasingly affordable, particularly in comparison to the cost of spectrum.
References:
¹ibid
²Derived in Astrapi Technical Report R-2013-1: Prothero, J.D. (2013). Hardware complexity of non-periodic signal modulation
Astrapi Corporation
100 Crescent Court, Suite 700
Dallas, TX 75201
