![]()
Astrapi® has introduced a ground-breaking technique for constructing and analyzing signals using sinusoidals with continuously-varying amplitude. Instantaneous Spectral Analysis (ISA) is a sharp break from the existing practice of
representing signals as sinusoidals which have constant amplitude over some period of time. With ISA, it is possible to construct signals using only sinusoidals in a limited frequency range that can convey many times more independent
amplitude values (and therefore information) than is possible with standard signal modulation.
Data Transmission Using Polynomials
Any signal can be described as a polynomial, which provides a smooth curve through some set of transmitted amplitude values. ISA is an entirely new technique that can construct any polynomial using a limited number of sinusoidals all having tightly-bounded frequencies. Using ISA, any signal transmitted in time “T” can be constructed using only sinusoidals with smoothly time-varying amplitudes and
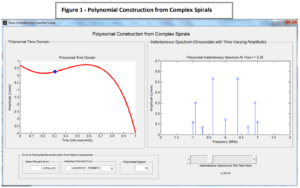
frequencies of 1/T or less. Figure 1, generated from Astrapi’s ISA Toolkit, shows an example of a random 15th degree. polynomial with a transmission time of 1 µs that is
constructed entirely from frequencies of 1 MHz or less.
The right panel displays the instantaneous amplitude values for the 9 sinusoidals used to construct the polynomial at time 𝑡 = 0.3. The ISA construction of the polynomial agrees with direct evaluation of the polynomial, generated from itscoefficients, to much less than 1% error across the entire evaluation interval.
Relationship to the Sampling Theorem
In the Figure 1 example, a random polynomial of degree 15 specifies 16 independent amplitude values. For transmission time T = 1 µs and bandwidth B = 1 MHz, the number of transmitted amplitude values is 16×B×T. According to the sampling theorem, the maximum number of amplitude levels that could be reconstructed without aliasing is 2×B×T, so the ISA construction shown above exceeds the generally accepted data throughput limit by a factor of 8. How is this possible?
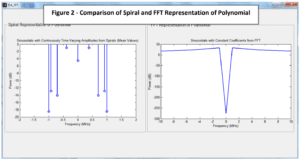
The proof of the sampling theorem implicitly assumes that a signal is represented by sinusoidals with constant amplitude, which ISA does not do. It is correct that the above polynomial could not be constructed in 1 MHz bandwidth using constant
amplitude sinusoidals, as the comparison between the ISA and Fourier Transform (FT) representations of this polynomial shows in Figure 2. The FT logarithmic power plot on the right shows power usage that is essentially flat from 1 MHz to 10 MHz. This is not surprising, since from the sampling theorem transmitting 16 amplitude values in 1 microsecond requires at least 8 MHz of bandwidth using sinusoidals with constant coefficients. By contrast, the ISA representation of the polynomial shown in the left panel has no sinusoidal with power outside of 1 MHz.
What Does This Mean for Channel Packing?
We are used to thinking of bandwidth as being defined by what is produced by an FT. Actually; however, what an FT tells us is “if you want to represent this time-domain signal using sinusoidals with constant amplitude, this is the range of frequencies and their amplitudes that you will have to use.” As we have seen, ISA allows us to construct a signal using a much smaller frequency range by using continuously varying sinusoidal amplitudes. From an economic perspective, bandwidth usage is defined by channel packing separation. How closely can two channels be placed to each other in the spectrum without interfering with each other? For instance, if
we put a traditional signal 1 MHz above the ISA example (rather than the 8 MHz minimum that the sampling theorem implies is necessary), will either impair the other? The ISA signal will not be impaired because it neither generates nor requires frequencies outside of its 1 MHz band.
The traditional signal will not be affected because the ISA signal does not modulate sinusoidals outside of the 1 MHz ISA band. The time-variation of the ISA signal will not affect the traditional signal because it has to be prepared to deal with amplitude variation in neighboring channels in any case, as always occurs in standard communication due to symbol boundaries and channels switching from dormant to active.
The implication is that the 1 MHz bandwidth requirement for the ISA construction of the polynomial example, shown in Figures 1 & 2, at least 8 times better than what would be required with standard signal modulation, is economically meaningful.
ISA Technology Status
ISA is implemented in a functioning MATLAB® toolkit that demonstrates in detail its operations and competitive advantage over traditional signal modulation techniques. It was pioneered by Astrapi, which owns foundational patents, issued and pending, that protect this technology worldwide. ISA and the generation of signals from continuously amplitude-changing sinusoidals, termed Spiral Modulation, are based on a solid mathematical theory arising from a new generalization of Euler’s formula, the foundational mathematics for the telecommunications.
Technology Roadmap
Astrapi technology is pre-product. Our business model is based on IP licensing and R&D services. We will collaboratively partner with other companies in order to help them to bring product to market based on Astrapi technology.
Contacts:
[email protected]
(214)-718-0325
www.astrapi-corp.com
